
Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License. Use the information below to generate a citation. Then you must include on every digital page view the following attribution: If you are redistributing all or part of this book in a digital format, Then you must include on every physical page the following attribution: Use graphing to solve quadratic equations A quadratic equation has two roots if its graph has two x-intercepts A quadratic equation has one root it its graph. If you are redistributing all or part of this book in a print format, Want to cite, share, or modify this book? This book uses the We can see this by expanding out the general form and setting it equal to the standard form. It also displays various information about the function. The standard form and the general form are equivalent methods of describing the same function. The applet allows the user to plot the quadratic function using sliders controlling, and. But if | a | 1, | a | > 1, so the graph becomes narrower. If h > 0, h > 0, the graph shifts toward the right and if h 1, | a | > 1, the point associated with a particular x - x - value shifts farther from the x-axis, so the graph appears to become narrower, and there is a vertical stretch. If k > 0, k > 0, the graph shifts upward, whereas if k 0, k > 0, so the graph is shifted 4 units upward.

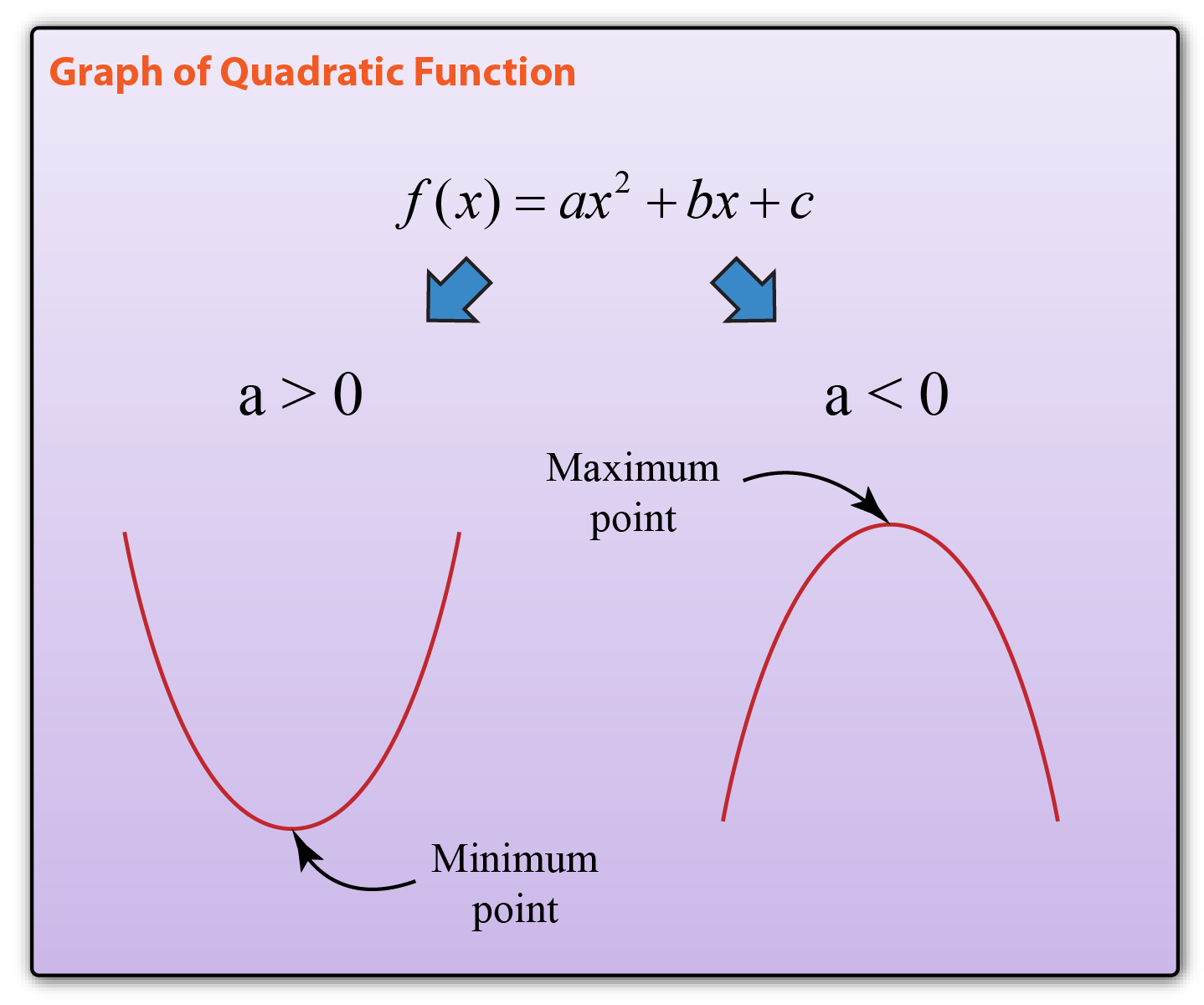
The x - x - intercepts, those points where the parabola crosses the x - x - axis, occur at ( −3, 0 ) ( −3, 0 ) and ( −1, 0 ). When the a is no longer 1, the parabola will open wider, open more narrow, or flip 180 degrees. In the parent function, y x2, a 1 (because the coefficient of x is 1). For a parabola that opens upward, the vertex occurs at the lowest point on the graph, in this instance, ( −2, −1 ). Another form of the quadratic function is. The vertex always occurs along the axis of symmetry. This also makes sense because we can see from the graph that the vertical line x = −2 x = −2 divides the graph in half. The axis of symmetry is x = − 4 2 ( 1 ) = −2. If a 0, a > 0, the parabola opens upward. If a > 0, a > 0, the parabola opens upward. Where a, b, a, b, and c c are real numbers and a ≠ 0. These features are illustrated in Figure 2.į ( x ) = a x 2 + b x + c f ( x ) = a x 2 + b x + c When we divide the independent variable of a function by a constant number, c, the effect on its graph is horizontal scaling (stretching or compressing). A quadratic function is one of the form f(x) ax2 + bx + c, where a, b, and c are numbers with a not equal to zero. The graph is also symmetric with a vertical line drawn through the vertex, called the axis of symmetry. In either case, the vertex is a turning point on the graph. If the parabola opens down, the vertex represents the highest point on the graph, or the maximum value. If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function. One important feature of the graph is that it has an extreme point, called the vertex. The graph of a quadratic function is a U-shaped curve called a parabola. Working with quadratic functions can be less complex than working with higher degree functions, so they provide a good opportunity for a detailed study of function behavior. In this section, we will investigate quadratic functions, which frequently model problems involving area and projectile motion. So, given a quadratic function, y ax2 + bx + c, when a is positive, the parabola opens upward and the vertex is the minimum value. The cross-section of the antenna is in the shape of a parabola, which can be described by a quadratic function. (credit: Matthew Colvin de Valle, Flickr)Ĭurved antennas, such as the ones shown in Figure 1, are commonly used to focus microwaves and radio waves to transmit television and telephone signals, as well as satellite and spacecraft communication. The general form of a quadratic function presents the function in the formį\left(x\right)=ak\right) is the vertex.Figure 1 An array of satellite dishes. It crosses the y-axis at (0, 7) so this is the y-intercept. This parabola does not cross the x-axis, so it has no zeros. We called equations like this linear equations. For a quadratic function f(x)ax2+bx+c f ( x ) a x 2 + b x + c, if a>0 a > 0 the graph opens up and if a<0 a < 0 the graph opens down. We have graphed equations of the form Ax+B圜. The x-value where the graph crosses the x-axis can also be used to. The axis of symmetry is the vertical line that intersects the parabola at the vertex. Recognize the Graph of a Quadratic Equation in Two Variables. You can find when y 0 on the table, and the x-value at that point will solve the function. The vertex is the turning point of the graph.


 0 kommentar(er)
0 kommentar(er)
